1. 게임이론 (Game Thoery)

Shapley Value에 대해 알기위해서는 게임이론에 대해 먼저 이해해야한다. 게임이론이란 우리가 아는 게임을 말하는 것이 아닌 여러 주제가 서로 영향을 미치는 상황에서 서로가 어떤 의사결정이나 행동을 하는지에 대해 이론화한 것을 말한다. 즉, 아래 그림과 같은 상황을 말한다. ¹

게임이론은 크게 네 가지 종류로 분류할 수 있다.

2. Shapley value

게임이론을 바탕으로 하나의 특성 대한 중요도를 알기위해 여러 특성들의 조합을 구성하고 해당 특성의 유무에 따른 평균적인 변화를 통해 얻어낸 값이 바로 shapley value이다.

Interpretable Machine Learning의 내용을 기반으로 번역하여 정리해보자면 예를 들어 아파트 가격을 예측하기위한 머신러닝 모델이 있다고 가정하자. 어떤 아파트에 대해서 집값을 300,000만 유로라고 모델은 예측했다. 이 아파트는 50평방 미터의 크기이고 2층에 위치하며 그처에 공원이 있고 고양이는 출입금지이다.

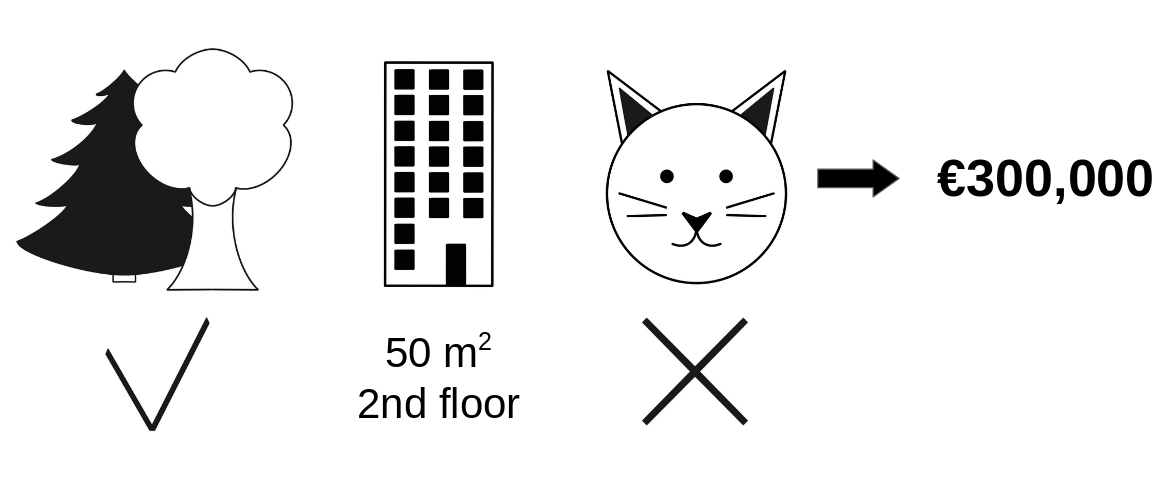
50평방 미터의 크기이고 2층에 위치하며 그처에 공원이 있고 고양이는 출입이 금지된 아파트에 대해 예측된 가격은 300,000만 유로이다. 이제 각 특성들이 예측치에 얼마나 기여를 했는지 설명해보도록 한다.

모든 아파트의 평균 예측가는 310,000 유로이다. 그렇다면 평균가와 비교하여 각 특성들이 얼마나 예측값에 기여를 한것일까?

선형모델을 사용하면 쉽게 알 수 있다. 선형모델에서 각 특성의 영향력은 각 특성값과 그에대한 가중지(선형회귀의 경우 coefficient를 말함)을 곱한 값이다. 선형모델은 인과성을 가지고 있기때문에 이렇게 단순히 가중치를 통해서 영향력을 바로 확인할 수 있다. 그러나 조금 더 복잡한 모델의 경우 (비선형적인 모델들) 다른 방법이 필요하다. 예를 들어 LIME의 경우는 영향력을 확인하기위해 지역적으로 선형모델을 적용하는 방법을 제안한다. 또다른 방법은 바로 게임이론을 적용하는 것이다. 1953년에 Shapley가 쓴 논문에서 처음 Shapley value라는 단어가 언급되었다 ². 이 방법은 총 지불금(payout)에 각 선수들(players)의 기여도에 따라 선수의 지불금을 정의하는 것이다.

지불금? 선수들? 게임? 머신러닝과 어떤 관계인가? 여기서 “게임”은 하나의 인스턴스(관측치)에 대한 예측을 말한다. “이득(gain)”은 모든 데이터로부터 얻은 평균예측값에서 하나의 관측치로부터 얻은 예측값을 뺀 값이다. “선수들”는 예측값을 얻는데 사용한 각 특성들을 말한다. 아파트 예측에 대한 얘기를 계속해보자면 park-nearby, cat-banne, area-50 and floor-2nd 는 모두 300,000 유로라는 예측에 사용된 특성들이다. 우리가 알고싶은 것은 평균가 310,000 유로와 예측값 300,000 유료의 차이인 -10,000 유로에 대한 것이다.

결과적으로 먼저 얘기하자면 park-nearby는 30,000 유로, size-50은 10,000 유로, floor-2nd는 0유로, cat-banned는 - 50,000 유로만큼 영향을 주었다.

하나의 특성에 대한 Shapley value는 어떻게 계산할까?

Shapley value는 모든 가능한 조합에 대해서 하나의 특성의 기여도를 종합적으로 합한 값이다.

첫 번째로 park-nearby와 size-50을 추가했을때 cat-banned의 기여도를 평가한다고 하자. 그러면 처음에는 park-nearby, size-50 and cat-banned를 사용하여 무작위로 여러 아파트들에 대한 예측을 해보고 floor 특성에 대한 가치를 확인한다. floor-2nd를 floor-1st로 바꿔가며 평가했고 310,000 유료에 대한 예측값은 변하지 않았다. 두 번째는 앞서 사용한 특성들에서 cat-banned값을 cat-allowed 값과 바꿔가며 여러 데이터들을 예측해본다. 그 결과 아래의 그림처럼 park-nearby와 size-50으로 이전에 310,000 유로로 예측한 아파트에 대해 320,000 유로로 예측하였다. 이를 통해 cat-banned의 기여도는 - 10,000 유로로 계산할 수 있다. 이러한 평가방식은 무작위로 선택된 아파트들의 가치에 의해 계산된것이다. 이 값은 반복적으로 계속 수행할수록 더 정확한 가치를 얻을 수 있다.

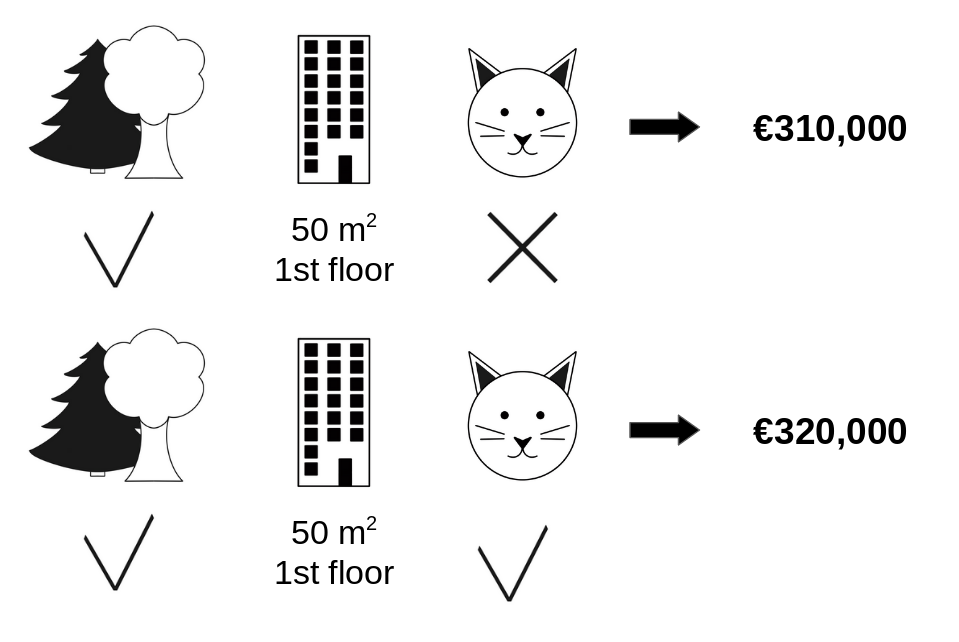
하나의 표본을 반복하여 "park-nearby" 와 "size-50"의 연합에 "cat-banned"를 추가했을때 기여도를 측정

위와 같은 계산 과정을 모든 가능한 연합에 대해서 반복한다. Shapley value는 모든 가능한 연합에 대한 모든 한계 기여도(marginal contributions)의 평균이다. 특성의 수가 늘어날 수록 연산 시간은 지수적으로 증가한다. 연산 시간을 조절할 수 있는 해결책 중 하나는 가능한 연합들의 몇개 샘플만 사용하는 것이다.

아래 그림은 cat-banned의 Shapley value를 계산하기위한 모든 특성들의 조합을 보여준다. 첫 번째 행은 어떠한 특성도 사용하지 않는다는 뜻이다. 두 번째, 새 번째 그리고 네 번째는 연합의 크기가 커짐과 함께 \(\shortmid\) 로 구분하여 서로 다른 연합을 나타낸다. 모든 가능한 연합은 아래와 같다.

• No feature values
• park-nearby
• size-50
• floor-2nd
• park-nearby+size-50
• park-nearby+floor-2nd
• size-50+floor-2nd
• park-nearby+size-50+floor-2nd

각 연합에 대해서 cat-banned가 포함된 연합과 포함되지 않은 연합의 아파트 예측 가격을 계산하고 한계 기여도를 계산하여 차이를 구한다. Shapley value는 한계 기여도의 (가중) 평균이다. 기계학습에서 예측치를 구하기위해 연합에 포함되지 않은 특성값은 아파트 데이터셋에서 무작위로 추출해서 대체한다.

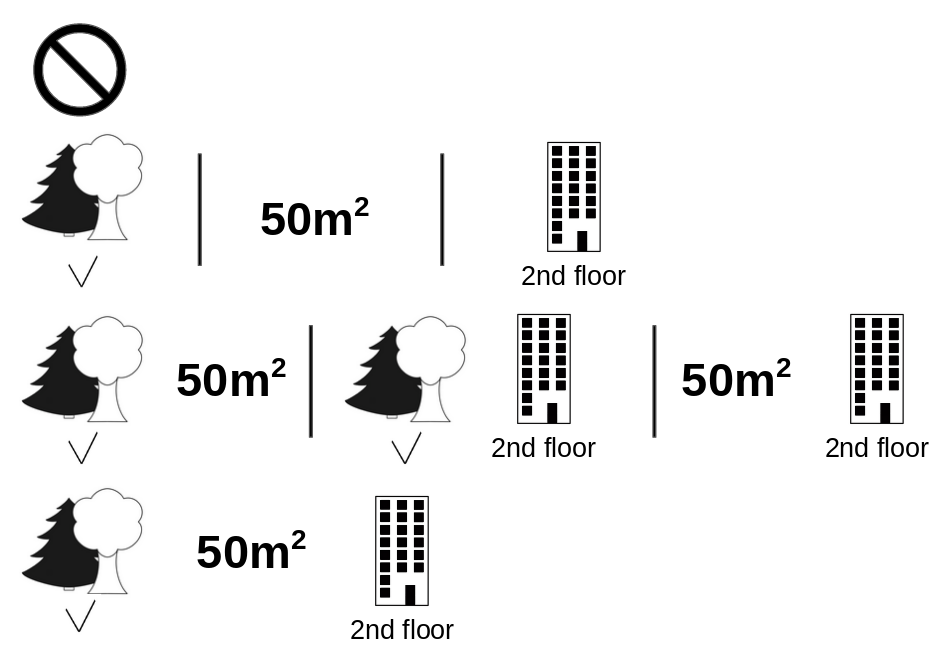
모든 특성값을 고려해서 Shapley value를 얻기위해서는 먼저 각 특성값에 대해 평균값으로부터 예측값의 차이를 나타내는 분포를 얻어야한다.

3. Examples and Interpretation

특성값 \(j\) 에 대한 Shapley value의 해석 : \(j\) 번째 특성값은 데이터셋에 대한 평균 예측값과 비교하여 특정 관측치를 예측하는데 \(\phi_j\) 만큼의 기여도를 가진다.

Shapley value는 분류(classification) 문제와 회귀(regression) 문제 모두 적용가능하다.

첫 번째 예제에서는 cervical cancer를 random Forest로 예측한 결과에 대해서 분석하기위해 Shapley value를 사용했다.

cervical cancer 데이터에서 여성에 대한 Shapley values. 이 여성의 예측치는 0.57로 암 발병 확률이 평균 예측치인 0.54보다 0.03 더 높다. 진단된 STDs의 값이 확률값을 가장 크게 상승시킨다. 기여도의 합은 해당 예측값과 전체 예측값(0.54)과의 차이이다.

두 번째 예제로는 bike rental 데이터에 대해서 일별 자전거 대여수를 예측하기위해 주어진 데이터인 날씨와 일별 정보를 가지고 random forest를 사용하여 학습했다. 아래 설명을 위한 그래프는 특정 날짜에 대한 random forest의 예측값에 대해 만들었다.

day 285에 대한 Shapley values. 이 날은 예측된 자전거 대여수가 2409로 평균 예측값인 4518보다 2108만큼 더 작다. 이 날 기온은 긍정적인 기여도를 가진다. 기여도의 합은 해당 예측값과 전체 예측값(4518)과의 차이이다.

Shapley value를 해석할 때 주의할 점이 있다. Shapley value는 서로 다른 특성들의 조합으로 얻은 예측값에 대한 해당 특성(기여도를 알고싶은 특성)의 기여도를 평균하여 계산한 값이다. 단순히 학습된 모델로부터 특성을 제외했을때 나타난 예측값의 차이를 말하는 것이 아니다.

4. The Shapley Value in Detail

이 부분에서는 궁금해하는 독자들을 위해 Shapley value의 연산과정과 정의에 대해서 더 깊게 설명하도록 한다. 만약 기술적인 부분에 흥미가 없다면 바로 “장점과 단점”으로 건너뛰면 된다.

각 특성값이 각 데이터에 대한 예측값에 얼마나 영향을 미치는지 궁금할 수 있다. 선형 모델의 경우 각각의 영향 계산하기가 쉽다. 아래 수식을 예로 들자면 특정 관측치에 대한 선형 모델의 예측 결과로 볼 수 있다.

\[\hat{f}(x) = \beta_{0} + \beta_{1}x_{1} + \dotsc + \beta_{p}x_{p}\]

여기서 \(x\)가 기여도를 계산하기 원하는 특정 관측치이다. 각 \(x_{j}\)는 특성값이다. \(j = 1, \dotsc ,p\) 일 때, \(\beta_j\) 는 특성 \(j\)에 대한 가중치이다.

예측값 \(\hat{f}(x)\)에서 \(j\) 번째 특성의 기여도 \(\phi_j\) :

\[\phi_j(\hat{f})=\beta_jx_j-E(\beta_jX_j)=\beta_jx_j-\beta_jE(X_j)\]

여기서 \(E(\beta_jX_j)\)는 특성 \(j\)에 대해 평균 추정 효과이다. 기여도는 평균 효과와 각 특성 효과의 차이이다. 오우! 그렇다면 이제 각 특성이 예측값에 얼마나 기여했는지 알 수 있다. 하나의 관측치에 대한 모든 특성의 기여도를 계산한다면 아래와 같이 나타낼 수 있다.

\[\begin{aligned} \sum^p_{j=1}\phi_j(\hat{f}) &= \sum^p_{j=1}(\beta_jx_j-E(\beta_jX_j)) \\ &= (\beta_0 + \sum^p_{j=1}\beta_jx_j) - (\beta_0 + \sum^p_{j=1}E(\beta_jX_j)) \\ &= \hat{f}(x) - E(\hat{f}(X)) \end{aligned}\]

이 결과값은 특정 데이터 \(x\)에서 평균 예측값을 뺀 값이다. 특성 기여도는 음수도 나올 수 있다.

이러한 과정을 선형 모델뿐만 아니라 다른 모델에도 똑같이 적용할 수 있을까? 이 과정을 model-agnostic으로 활용할 수 있는지 알아보자. 보통은 모델의 유형에 따라 비슷한 가중치를 갖지 않기 때문에 다른 방법이 필요하다.

예상치 못한 도움 : 협동 게임 이론 (cooperative game theory). Shapley value는 어떤 기계학습 모델이든지 단일 예측치로부터 특성의 기여도를 계산하기위한 방법이다.

4.1. The Shapley Value

Shapley value는 집합 S에 대한 선수(players)의 값 함수의 값(a value function val)으로 정의된다.

특성값의 Shapley value는 모든 가능한 특성값의 조합에 대해서 가중치를 부여하고 합하여 계산된 지불금(payout)에 대한 기여도이다.

\[\phi_j(val) = \sum_{S\subseteq\{x_1,\dotsc,x_p\}\setminus\{x_j\}}\frac{|S|!(p-|S|-1)!}{p!}(val(S\cup\{x_j\})-val(S))\]

여기서 S는 모델에 사용된 특성들의 부분집합, x는 설명을 위한 관측치의 특성값 벡터 그리고 p는 특성의 수이다. val_x(S)는 집합 S에 포함되지 않은 특성을 모두 한계화(marginalized)한 집합 S의 특성값들에 대한 예측치이다.

\[val_{x}(S)=\int\hat{f}(x_{1},\dotsc,x_{p})d\mathbb{P}_{x\notin{}S}-E_X(\hat{f}(X))\]

예를 들자면 특성 x1, x2, x3 그리고 x4를 학습한 기계학습 모델이 있고 특성 x1과 x3를 포함하는 연합(the coalition) S에 대한 예측치를 평가한다고 하자.

\[val_{x}(S)=val_{x}(\{x_{1},x_{3}\})=\int_{\mathbb{R}}\int_{\mathbb{R}}\hat{f}(x_{1},X_{2},x_{3},X_{4})d\mathbb{P}_{X_2X_4}-E_X(\hat{f}(X))\]

위 수식을 보면 선형모델의 특성별 기여도를 계산하는 과정과 비슷해보인다.

여기서 많이 사용되는 “값(value)”이라는 단어에 대해 오해하지 않아야한다. : 특성값은 특성과 관측치에 대한 숫자형 또는 범주형 값이다. Shapley value는 예측치에 대한 특성 기여도이다. 값 함수(the value function)은 선수들의 연합(coalitions of players)에 대한 지불금 함수(the payout function)이다.

Shapley value는 Efficiency, Symmetry, Dummy 그리고 Additivity를 모두 만족시키는 유일한 attribution method이고 이 네 가지를 공정한 지불금(a fair payout)에 대한 정의로서 간주될 수 있다.

Efficiency

특성 기여도들은 반드시 x에 대한 예측치와 평균의 차이를 더한 값이어야한다.

\[\sum\nolimits_{j=1}^p\phi_j=\hat{f}(x)-E_X(\hat{f}(X))\]

Symmetry

두 개의 특성값 \(j\) 와 \(k\)의 기여도는 모두 같은 가능한 연합에 기여했다면 값이 같아야 한다.

\[val(S\cup\{x_j\})=val(S\cup\{x_k\})\]

모든 경우에 대해 아래와 같은 가정하에서

\[S\subseteq\{x_{1},\dotsc,x_{p}\}\setminus\{x_j,x_k\}\]

기여도가 같아야 한다.

\[\phi_j=\phi_{k}\]

Dummy

예측값에 영향이 없는 특성 \(j\) 는 (어떤 특성값의 연합에 추가되거나 안되거나) Shapley value는 0이어야 한다.

\[val(S\cup\{x_j\})=val(S)\]

모든 경우에 대해 아래와 같은 가정하에서

\[S\subseteq\{x_{1},\dotsc,x_{p}\}\]

기여도는 0이어야 한다.

\[\phi_j=0\]

Additive

결합된 지불금인 \(val+val^+\)이 있는 게임에서 각가의 Shapley value는 아래 수식을 따른다.

\[\phi_j+\phi_j^{+}\]

많은 의사결정나무를 평균내어 예측을 하는 Random forest를 학습했다고 가정해보자. Additivity 속성은 각 특성값에 대해서 Shapley value를 각 트리별로 개별적으로 계산할 수 있고 평균내어 random forest에서 특성값들에 대해 Shapley value를 구할 수 있다는 것을 말한다.

4.2. Intuition

직관적으로 Shapley value를 이해할 수 있는 방법은 이렇게 설명해 볼 수 있다. : 특성값이 무작위로 나열되어 방에 들어온다. 방에 있는 모든 특성값은 게임에 참여한다(= 예측치에 기여한다). 특성값의 Shapley value는 특성값이 연합에 참여할때 이미 방에 있던 연합이 얻은 예측치의 평균적인 변화이다.

4.3. Estimating the Shapley Value

특성값의 모든 가능한 연합은 정확한 Shapley value를 계산하기위해서 j번째 특성이 있는 것과 없는 것 모두 평가되어야만 한다. 특성 수가 커짐에 따라 가능한 연합의 수가 기하급수적으로 늘어나기때문에 Shapley value를 계산하는 정확한 방법이 오히려 문제가 될 수 있다. Strumbelj et al. (2014)는 몬테카를로 샘플링(Monte-Carlo sampling)으로 추정치를 구하는 방법을 제안한다 ³.

\[\hat{\phi}_{j}=\frac{1}{M}\sum_{m=1}^M\left(\hat{f}(x^{m}_{+j})-\hat{f}(x^{m}_{-j})\right)\]

여기서 \(\hat{f}(x^{m}_{+j})\) 는 \(x\)에 대한 예측치이다. 단, 특성 \(j\)의 값에 대해서는 제외하고 나머지 특성값의 아무값을 무작위로 선정한 관측치 z로부터 특성값을 추출하여 대체하였다. \(x\) 벡터 \(x^{m}_{-j} 는 x^{m}_{+j}\)와 거의 비슷하다. 대신 \(x^{m}_{j}\) 또한 샘플링된 \(z\)로부터 대체된다. 각 \(M\)개의 새로운 관측치는 두 관측치로부터 형성된 “프랑켄슈타인 괴물(Frankenstein Monster)”같은 것이다.

단일 특성치로부터 Shapley value의 추청치를 근사하게 구하는 방법

• Output: Shapley value for the value of the j-th feature
• Required: Number of iterations M, instance of interest x, feature index j, data matrix X, and machine learning model f
• For all m = 1,…,M:
  • Draw random instance z from the data matrix X
  • Choose a random permutation o of the feature values
  • Order instance x: \(x_o=(x_{(1)},\dotsc,x_{(j)},\dotsc,x_{(p)})\)
  • Order instance z: \(z_o=(z_{(1)},\dotsc,z_{(j)},\dotsc,z_{(p)})\)
  • Construct two new instances
    • With feature j: \(x_{+j}=(x_{(1)},\dotsc,x_{(j-1)},x_{(j)},z_{(j+1)},\dotsc,z_{(p)})\)
    • Without feature j: \(x_{-j}=(x_{(1)},\dotsc,x_{(j-1)},z_{(j)},z_{(j+1)},\dotsc,z_{(p)})\)
  • Compute marginal contribution: \(\phi_j^{m}=\hat{f}(x_{+j})-\hat{f}(x_{-j})\)
• Compute Shapley value as the average: \(\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\)

위 과정을 풀어서 설명하자면 첫 번째로 기여도를 구하고 싶은 특성 x의 관측치(instance of interest \(x\)), 특성 인덱스 \(j\)(a feature \(j\)) 그리고 반복횟수 \(M\)(the number of iterations \(M\))을 구한다. 각 반복시마다 랜덤하게 뽑힌 관측치 \(z\) (a random instance \(z\))가 데이터로부터 선택된다. 그리고 랜덤하게 특성을 나열한다. 두 번째는 앞서 뽑은 특성 \(x\)와 \(z\)를 랜덤하게 조합하여 새로운 관측치를 만든다. \(x_+j\) 는 기여도를 구하고싶은 특성이 포함된 관측치이고 이때 z로 우선 관측치를 나열하고 이후 \(j\) 번째 특성을 대체한다. \(x_-j\)는 이와 반대로 \(j\)번째 특성을 제외한다. 그리고 두 관측치를 통해 나온 예측값의 차이를 계산한다.

정확한 계산과정에 대해서는 참고자료를 통해 확인하길 바란다.

\[\phi_j^{m}=\hat{f}(x^m_{+j})-\hat{f}(x^m_{-j})\]

모든 차이를 계산하고 평균으로 계산한다.

\[\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\]

모든 Shapley value는 이와같은 과정을 각 특성마다 반복하며 계산된다.

5. Advantages

Shapley values의 Efficiency 속성에 따라 각 예측치와 평균 예측치간의 차이는 각 관측치의 특성값 사이에 공평하게 분포되어있다. 이 속성은 LIME같은 방법과 Shapley value를 구분해준다. LIME은 예측치가 특성들 간의 공평하게 분포되어 있지 않다. Shapley value는 모델 전체를 완전히 설명할 수 있는 유일한 방법일 것이다. Shapley value는 확고한 이론적 기반과 공평하게 효과가 분포해있기 때문에 EU의 “right to explanations”와 같이 법률이 설명을 필요로하는 상황에서 사용할 수 있는 유일한 합법적인 방법일 것이다.

Shapley value는 대조 설명(contrastive explanations)이 가능하다. 즉, 전체와 하나의 관측치를 비교하여 영향도를 구할 수 있고 전체 데이터의 일부분 또는 다른 하나의 인스턴스와 비교해서도 영향도를 구할 수 있다. 이 대조성(contrativeness)는 LIME같은 지역적 모델(local model)에 없는 장점이다.

Shapley value는 이론적인 배경이 탄탄하다. Efficiency, symmetric, dummy 그리고 addictivity와 같은 공리들이 설명성에 합리적인 기반을 제공한다. LIME같은 방법들은 기계학습 모델이 지역적으로 선형성을 나타낸다고 가정하지만 어디에도 왜 그렇게 가정하는지에 대한 이론적 기반이 없다.

특성값에 의한 게임으로 예측을 설명한다는 것이 정말 놀랍다.

6. Disadvantages

Shapley value는 연산량이 너무 많다. 현실의 문제들 중 99.9%에서는 추정방법만이 사용가능하다. 특성들의 가능한 조합(2^k)과 특성의 “결측(absence)”은 아무 관측치로 대체하는 것(이로인해 Shapley value 추청값의 분산이 증가한다.)까지 모두 고려하기 때문에 연산 비용이 너무 크다. 연합의 지수적 크기는 샘플링과 반복횟수 M을 제한해서 대처할 수 있다. M을 줄이는 것만으로도 연산 시간을 줄일 수 있지만 Shapley value의 분산을 키울 수 있다. M에 대한 최적의 수가 따로 정해진건 없다. M은 Shapley value를 정확히 추정하기위해 크면 클 수록 좋다. 그러나 적당한 시간에 계산을 할 수 있는 정도로 정하면된다. Chernoff bounds를 기반으로 M을 선택할수도 있지만 기계 학습 예측을 위해 Shapley values를 구하는데 사용하는 경우는 본적이 없다.

Shapley value는 잘못 해석될 수 있다. 앞서 말한 주의사항처럼 단순히 기여도를 알고싶은 특성을 모델에서 제외했을때 생기는 차이로 Shapley value라고 생각될 수 있다. 그러나 다시 말하자면 Shapley value는 로 다른 특성들의 조합으로 얻은 예측값에 대한 해당 특성(기여도를 알고싶은 특성)의 기여도를 평균하여 계산한 값이다.

sparse한 설명성(적은 수의 특성에 대한 설명)을 원한다면 Shapley value를 사용하는 것은 잘못된 방법이다. Shapley value 방법으로 계산된 설명은 항상 모든 특성을 사용한다. 사람들은 LIME과 같이 선택적인 설명을 선호한다. 비전문가가 사용하기에는 LIME이 더 적절한 설명 방법일 수 있다. 또는 2016년에 나온 SHAP을 사용하는것도 좋은 방법이다 ⁴. SHAP은 Shapley value를 기반으로 하는 방법이고 적은 수의 특성으로도 설명성을 나타낼 수 있다.

Shapley value는 LIME과 다르게 설명가능한 모델이 아닌 단순히 특성별 기여도를 나타내는 값이다. 즉 입력값의 변화에 따른 예측값의 변화를 설명하기 힘들다. 예를 들면 “내가 1년에 300 유로를 더 번다면 내 신용점수는 5 포인트만큼 오를거야”와 같은 설명이 불가능하다.

또 다른 단점으로는 새로운 데이터에 대해서 Shapley value를 계산할 때 생기는 문제점이다. 새로운 데이터에 대한 정보가 기존 데이터에 없게되면 이 값을 대체하기위한 진짜와 비슷한 가상의 데이터를 만들어야지만 이 문제를 해결할 수 있다.

다른 permutation을 기반으로한 해석 방법들과 같이 Shapley value는 특성간 상관관계가 있는 경우 비현실적인 관측치를 포함하는 것에서 어려움이 있다. 연합에서 특성값이 누락되는 것을 시뮬레이션하기위해 특성치를 한계화(marginalize)한다. 이 과정은 특성치의 한계 분포(marginal distribution)에서 값을 샘플링하여 구할 수 있다. 이 방법은 특성들이 서로 독립이면 문제가 되지 않지만 독립이 아닌 경우에는 관측치에 맞지 않은 특성값을 추출하게 될 수 있다. 그러나 이 방법으로 특성에 대한 Shapley value를 구할 수 있다. 내가 아는 한에서는 이러한 방법이 Shapley value에 어떤 의미가 있는지 어떻게 수정할 수 있을까에 대한 연구가 없었다. 한가지 방법으로는 상관관계가 있는 특성들을 같이 permute하여 특성들에 대한 하나의 Shapley value를 구하는 것이다. 또는 상관관계가 있는 특성들을 고려해서 샘플링 과정을 조정하는 방법이 있을 수 있다.

7. Software and Alternatives

Shapley value는 R 패키지인 iml에 구현되어있다.

Shapley value에 대해 대안으로 나온 추정 방법인 SHAP은 다음 챕터에서 소개한다.

또다른 패키지는 breakDown이다 ⁵. BreakDown은 예측치에 대한 각 특성의 기여도를 나타내고, step by step으로 계산한다. 다시 게임에 비유하자면 아무도 없는 팀에서 예측에 가장 큰 기여를 한 특성값을 하나씩 추가해가며 모든 특성이 추가될때까지 반복한다. 각 특성이 얼마나 기여를 했는지는 이미 팀에 있는 특성에 따라 결정되는데 이게 breakDown의 가장 큰 단점이다. Shalpey value 방법보다는 빠르고 교호작용이 없는 모델에 대해서만 결과가 똑같이 나온다.

---