1. Example

자궁경부암의 위험(the risk for cervical cancer)을 예측하기 위해 100개의 random forest classifier로 훈련했다. 개별적인 예측을 설명하기 위해 SHAP를 사용을 했으며, random forest는 Tree Ensemble이기 때문에 느린 KernelSHAP 방법 대신에 빠른 TreeSHAP 추정 방법을 사용하였다.

SHAP은 Shapley value를 계산하기 때문에 해석은 Shapley value와 동일하다. 그러나 Python shap 패키지는 다른 시각화 Tool를 함께 제공해준다(Shapley value와 같은 특성 기여도를 “힘(force)”으로서 시각화할 수 있다). 각 특성값은 예측치를 증가시키거나 감소시키는 힘을 나타낸다. 예측치는 기준선(baseline)에서 시작하며 Shapley value의 기준선(baseline)은 모든 예측의 평균이 된다. 아래 그림에서 각 Shapley value는 예측을 증가(양수 값) 또는 감소(음수 값)하는 방향으로 밀어낸다. 이러한 힘은 관측치의 실제 예측값에서 서로 균형을 맞춰준다.

다음 그림은 자궁경부암 데이터 세트를 사용했으며 두 여성에 대한 SHAP explanation force plots 을 보여준다.

SHAP values to explain the predicted cancer probabilities of two individuals

Case 1) 평균 예측 확률인 기준치는 0.06이다. 첫 번째 여성 0.06으로 낮은 자궁 경부암의 위험도를 가지고 있다. STD와 같은 위험 증가 효과는 연령(Age)과 같은 효과를 감소시켜 상쇄된다. Case 2) 두 번째 여성은 0.71의 높은 자궁 경부암의 위험도를 가지고 있다. 연령(Age)이 51세, 흡연하는 연수(years of smoking)가 34년의 특성이 여성의 자궁 경부암의 위험도를 증가시켰다.

각 예측치에 대한 설명입니다.

Shapley value는 전체에 대한 설명(global explanations)으로 합쳐서 나타낼 수 있다. 모든 경우에 대해 SHAP을 실행하면 Shapley value의 행렬을 얻을 수 있다. 이 행렬은 한 개의 관측치인 행과 한 개의 특성인 열(column)을 가진다. 이 Shapley value의 행렬을 분석하면 전체 모델을 해석할 수 있게 된다.

1.1. SHAP Feature Importance

SHAP feature importance의 원리는 간단하다. 절대값 Shapley value가 큰 특성이 가장 중요하며, global importance를 원하기 때문에 데이터 전체에서 특성 당 Shapley values의 절댓값 평균을 낸다.

\[I_j=\sum_{i=1}^n{}|\phi_j^{(i)}|\]

다음으로, 중요도를 줄임으로써 특성을 분류하고 시각화한다. 다음 그림은 자궁경부암(cervical cancer)을 예측하기 위해 이전에 훈련된 random forest로 SHAP feature importance를 보여준다.

SHAP feature importance measured as the mean absolute Shapley values

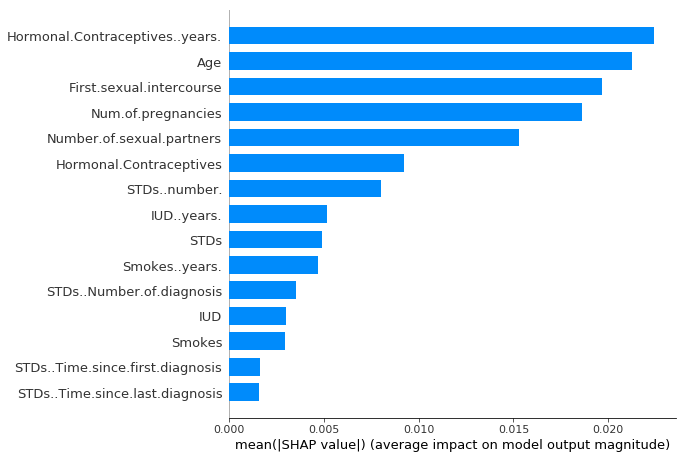
호르몬 피임약(hormonal contraceptives)을 복용한 연도 수는 가장 중요한 특성으로 예측되는 암 발생 확률의 절댓값은 평균 2.4% 포인트(x축 0.024)로 변하고 있다.

SHAP feature importance는 permutation feature importance의 대안이며, 두 가지 방법은 중요도 측정에서 가장 큰 차이점을 보인다. Permutation feature importance는 모델 성능의 감소에 기반을 두지만 SHAP은 특성 기여도의 크기에 기반을 둔다.

feature importance plot은 유용하지만 중요도에 아무런 정보를 포함하지 않아, 더 많은 정보를 주는 시각화를 보기위해서는 summary plot을 확인하면 된다.

1.2. SHAP Summary Plot

The summary plot는 특성 중요도(feature importance)와 특성 효과(feature effects)를 겹합한다. summary plot의 각 점은 특성에 대한 Shapley value와 관측치이며, x축은 Shapley value에 의해 결정되고 y축은 특성에 의해 결정된다. 색은 특성의 값을 낮음에서 높음까지 나타내며, 겹치는 점이 y축 방향으로 내포됨에 따라 특성 당 Shapley value의 분포를 알 수 있다. 또한, 특성은 중요도에 따라 정렬이 된다.

SHAP summary plot

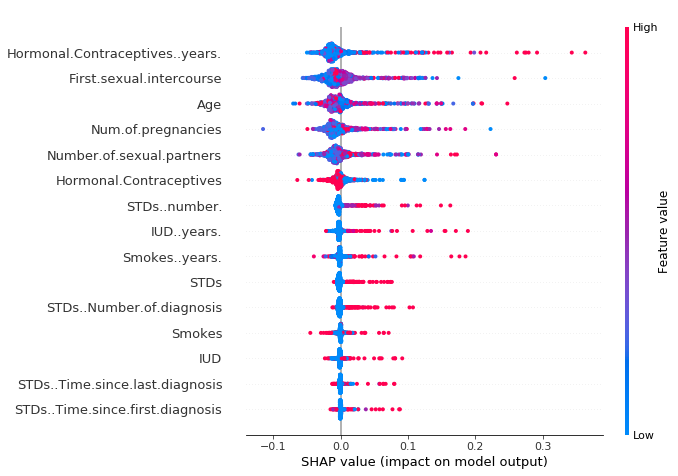
더 적은 연수의 호르몬 피임약(hormonal contraceptives)은 예측되는 암 위험도가 적이지고 더 많은 연수의 호르몬 피임약(hormonal contraceptives)은 암 위험도를 증가시킨다.

모든 효과는 모델의 행동을 설명하는 것이지 현실에서 반드시 인과관계가 있는 것은 아니다

summary plot에서 특성값과 예측에 미치는 영향 사이의 관계 지표를 볼 수 있다. 그러나 관계의 정확한 형태를 보기 위해서는 SHAP dependence plot을 보아야 한다.

1.3. SHAP Dependence Plot

SHAP feature dependence는 가장 단순한 global interpretation 시각화이다.

방법

1. 특성을 선택한다.
2. 각 관측치에 대해 특성 값을 x축에, 해당하는 Shapley value를 y축에 표시한다.

수학적으로 이 그래프는 다음의 점을 포함한다. \(\{(x_j^{(i)},\phi_j^{(i)})\}_{i=1}^n\)

다음의 그래프는 수년간 호르몬을 투여한 특성에 대한 SHAP feature dependence를 보여준다.

SHAP dependence plot for years on hormonal contraceptives

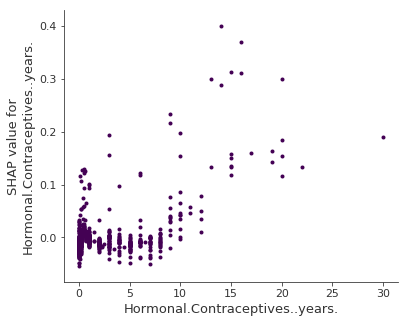
0년과 비교하여, 적은 년수의 호르몬 투여(hormonal contraceptives)는 예측된 암 확률도가 낮고 높은 년수의 호르몬 투여(hormonal contraceptives)는 예측된 암 확률도를 증가시킨다.

SHAP dependence plots은 partial dependence plots과 accumulated local effects의 대안이다. 그 이유는 PDP와 ALE은 평균적인 효과를 나타내지만 SHAP dependence은 Y축에 대한 분산도 보여주기 때문이다. 특히 상호작용의 경우 SHAP dependence plot은 Y축에서 훨씬 더 분산된다. 이러한 특성 상호작용을 강조하는 것으로 dependence plot은 개선될 수 있다.

1.4. SHAP Interaction Values

상호작용 효과는 개별 특성 효과에 대해 고려한 후에 각 효과를 결합한 특성 효과이다. 게임 이론의 Shapley 상호작용 지수는 다음과 같이 정의한다.

\[\phi_{i,j}=\sum_{S\subseteq\setminus\{i,j\}}\frac{|S|!(M-|S|-2)!}{2(M-1)!}\delta_{ij}(S)\]

\(i\neq{}j\)일때

\[\delta_{ij}(S)=f_x(S\cup\{i,j\})-f_x(S\cup\{i\})-f_x(S\cup\{j\})+f_x(S)\]

이 공식은 개별 효과를 고려한 후 순수 상호 작용 효과를 얻을 수 있도록 특성의 주효과를 뺀다. Shapley value 계산에서와 같이 가능한 모든 특성 연합(coalition) S에 대한 값을 평균낸다. 모든 특성에 대해 SHAP 상호 작용 값을 계산할 때, 관측치 당 하나의 행렬(M*M차원)을 얻는다. 여기서 M은 특성의 수를 나타낸다.

어떻게 상호 작용 지수를 사용할 수 있을까? 예를 들어, 가장 강한 상호작용이 있는 SHAP feature dependence 그래프에 자동으로 색상을 칠해줄 수 있다.

SHAP feature dependence plot with interaction visualization

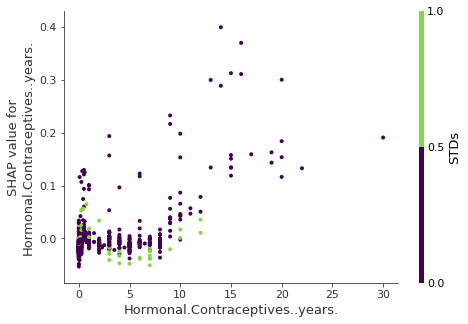
호르몬 피임약의 연수(Years on hormonal contraceptives)는 성병(STDs)과 상호작용을 한다. 호르몬 피임약의 연수(hormonal contraceptives)가 0에 가까운 경우 성병(STDs)의 발생 확률은 예상되는 암 위험을 증가시킨다. 수년간의 호르몬 피임약 복용(hormonal contraceptives)은 성병(STDs)에 걸릴 위험을 줄인다.

다시 말하지만, 이것은 인과 관계 모델이 아니다. 효과는 교란 요인에 의해 발생할 수 있다.(예를 들어, 성별과 낮은 암 위험은 더 많이 의사에게 방문하는것과 상관관계가 있을 수 있다. )

1.5. Clustering SHAP values

Shapley value를 사용하여 데이터를 군집화할 수 있다. 군집화의 목표는 유사한 관측치 그룹을 찾는 것이며 일반적으로 군집화는 특성을 기반으로 한다. 특성은 종종 다른 척도로 나타낸다. 예를 들어 높이는 미터, 색상 강도는 0에서 100 사이, 일부 센서 출력은 -1과 1 사이에서 측정 할수 있으며. 비교 할 수 없는 서로 다른 특성을 사용하면 관측치 간의 거리를 계산하는 것은 어려워진다.

SHAP clustering의 원리는 각 관측치의 Shapley value에서 군집화하는것 이며, 이는 유사성을 설명하여 관측치를 군집화하는 것을 의미한다. 모든 SHAP Value 단위는 prediction space의 단위다. 원하는 군집화 방법을 사용할 수 있으며, 다음 예제에서는 hierarchical agglomerative clustering을 사용하여 관측치를 정렬하였다.

아래의 plot은 여러 개의 force plots로 구성되며, 각 관측치의 예측에 따라 설명된다. the force plots를 수직으로 회전 시켜 군집화 유사성에 따라 나란히 배치하였다.

Stacked SHAP explanations clustered by explanation similarity

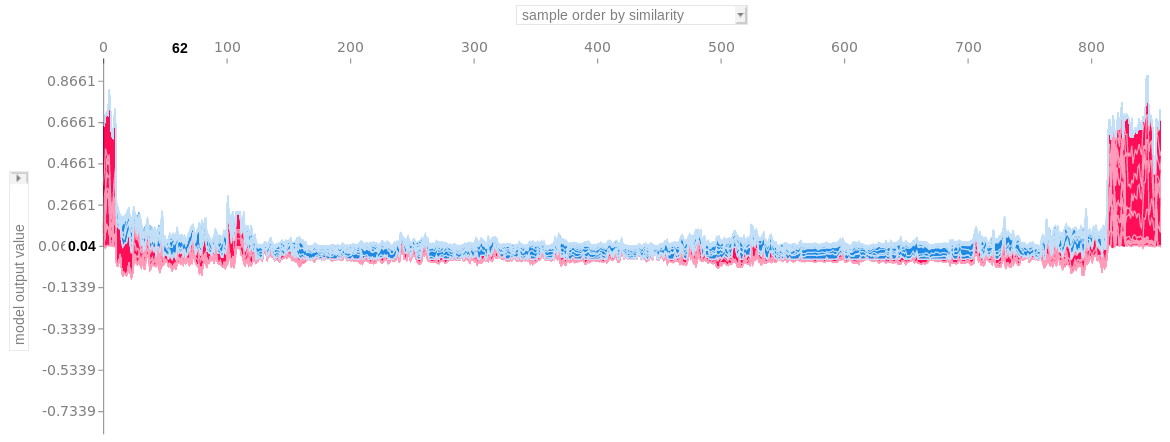
x축 각 위치는 관측치이다. 빨간색 SHAP Value는 예측을 증가시키고 파란색 SHAP Value는 예측을 감소시킨다. 오른쪽에 빨간색이 높은 군집은 높게 예측된 암 위험(cancer risk)이 있는 집단으로 확인 할 수 있다.