1. SHAP (SHapley Additive exPlanations)

Lundberg와 Lee가 제안한 SHAP (SHapley Additive exPlanations)은 각 예측치를 설명할 수 있는 방법이다¹. SHAP은 게임 이론을 따르는 최적의 Shapley Value를 기반으로한다.

1.1. SHAP이 Shapley values보다 더 좋은 이유

1. SHAP는 LIME과 Shapley value를 활용하여 대체한 추정 접근법인 Kernel SHAP와 트리 기반 모델을 위한 효율적인 추정 접근법인 Tree SHAP를 제안했다.
2. SHAP는 Shapley Value의 계산 방법을 기반으로 하여 데이터 셋의 전체적인 영역을 해석할 수 있는 많은 방법을 가지고 있다.

2. Definition

SHAP의 목적은 예측에 대한 각 특성의 기여도를 계산하여 관측치 x의 예측값을 설명하는 것이다. SHAP 설명 방법은 연합 게임 이론(coalitional game theory)을 사용하여 Shaply value를 계산하고 관측치(data instance)의 특성값은 연합에서 플레이어로서 역할을 한다. Shaply Value는 특성들 사이에 “지불(payout) (=예측(prediction))”을 공정하게 분배하는 방법을 알려준다. 예를 들어 tabular data에서 플레이어는 각각의 특성값이 될 수 있으며 특성값의 그룹이 될 수도 있다. 예를 들어 이미지를 설명하기 위해 픽셀을 수퍼 픽셀(픽셀들의 그룹)로 그룹화하고 수퍼 픽셀 간의 예측값의 분포를 확인할 수 있다. SHAP가 가져온 혁신 중 하나는 Shapley Values 설명이 additive feature method인 선형모델로 표현할 수 있다는 것이다. 이러한 점이 LIME과 Shapley Value을 연결 짓는다. SHAP에 대한 설명은 다음과 같이 수식으로 표현할 수 있다.

\[g(z')=\phi_0+\sum_{j=1}^M\phi_jz_j'\]

여기서 \(g\)는 설명 모델, \(z'\in\{0,1\}^M\)은 연합 벡터(coalition vector), M은 최대 연합 사이즈 그리고 \(\phi_j\in\mathbb{R}\)은 특성 \(j\)의 특성 기여도, Shapley value를 말한다. 여기서 얘기한 연합 벡터는 SHAP 논문에서는 “simplified features”라고 부른다. 이 단어는 상황에 따라 다르게 쓰이기 때문에 편한대로 선택해서 사용하면된다. 예를 들면 이미지 데이터에서는 픽센 단위가 아닌 수퍼 픽셀로 집계한다. 이러한 예시는 연합에 대한 설명으로 z에 대해서 생각해보는데 도움을 줄 수 있다. : 연합 벡터에서는 1은 특성값이 “존재(present)”, 0은 특성값이 “부재(absent)”라는 것을 뜻한다. 연합의 선형 모델로 표현해서 \(\phi\)의 계산식을 나타낼 수 있다. 관심있는 x에 대해 연합벡터 x’은 모두 1로 구성된 벡터이다. 즉, 모든 특성이 “존재”한다는 말이다. 수식을 단순화하자면 아래와 같이 표현할 수 있다.

\[g(x')=\phi_0+\sum_{j=1}^M\phi_j\]

이 공식은 Shapley value를 정리한 포스팅에서 찾을 수 있다. 실제 추정방법에 대해서는 이후 아래에서 더 설명한다. 추정하는 방법에 대해서 자세히 알아보기 전에 \(\phi\)의 속성을 먼저 확인해보도록한다.

Shapley value는 Efficiency, Symmetric, Dummy 및 Additivity의 특성을 만족시키는 유일한 방법(unique solution)이다. SHAP은 Shapley value를 기반으로 계산하기 때문에 이를 만족시킨다. SHAP 논문에는 SHAP 속성과 Shapley 속성 간에 차이가 있다. SHAP은 다음 세 가지 속성을 따른다.

2.1. ) Local accuracy

\[f(x)=g(x')=\phi_0+\sum_{j=1}^M\phi_jx_j'\]

만약 \(\phi_0=E_X(\hat{f}(x))\) 그리고 모든 \(x′_{j}\) 을 1로 정의한다면 local accuracy는 shapley value의 efficeicy 속성과 같게 된다.

\[f(x)=\phi_0+\sum_{j=1}^M\phi_jx_j'=E_X(\hat{f}(X))+\sum_{j=1}^M\phi_j\]

2.2. ) Missingness

\[x_j'=0\Rightarrow\phi_j=0\]

Missingness은 결측값(missing feature)이 0만큼의 영향력을 같는다는 것을 의미한다. \(x′_{j}\)는 결측값인 부분은 0으로 표시된 연합을 말한다. 연합 표기법에서 설명하기 위한 관측치의 모든 특성값 \(x′_{j}\)는 ‘1’ 이여야 한다. 0이 있으면 해당 관측치에 대한 특성값이 누락되었음을 의미한다. 따라서, 이 속성은 “normal”-Shapley Values의 속성에 포함되지 않는다. ‘왜 SHAP에 이러한 속성이 필요한가?’ 라는 물음에 Lundberg는 “minor book-keeping property”라고 말했다. (역자가 이해하기로는 결측치에 대한 부분을 처리하기 위해 결측치인 부분은 0으로 하여 shapley value를 계산할 때 기여도가 포함되지 않도록 하기 위함인듯하다.) \(x′_{j}=0\)으로 곱하기 때문에 수식적으로도 local accuracy를 위배하지 않고 결측치도 임의의 Shaply value을 가질 수 있다. Missingness 속성은 결측치가 0의 Shapley value를 갖도록 한다. 이는 일정 상수로만 해당이 된다.

2.3. ) Consistency

\(f_x(z')=f(h_x(z'))\)이고 \(z_{\setminus{}j'}\)에서 \(z_j'=0\)이라 하자. 두 모델 \(f\)와 \(f'\)은 이를 만족한다.

\[f_x'(z')-f_x'(z_{\setminus{}j}')\geq{}f_x(z')-f_x(z_{\setminus{}j}')\]

모든 입력값은 \(z'\in\{0,1\}^M\)이고, 아래와 같이 나타낼 수 있다.

\[\phi_j(f',x)\geq\phi_j(f,x)\]

consistency 속성은 모델이 변경되어도 특성값의 marginal contribution이 (다른 특성에 관계없이) 증가하거나 동일하게 유지되는 경우 shaply value도 증가하거나 동일하게 유지된다. 단 감소하는 것은 안 된다. Shapley value의 네 가지 속성은 Lundberg와 Lee의 부록에 자세히 설명되어 있다.

수식적으로는 아래와 같이 표현할 수 있다.

3. KernelSHAP

KernelSHAP은 관측치 x에 대한 각 특성값의 예측 기여도를 추정한다. KernelSHAP의 계산과정은 아래와 같이 5단계로 구성된다.

• 연합에서 샘플링하여 표본을 구한다. \(z_k'\in\{0,1\}^M,\quad{}k\in\{1,\ldots,K\}\), \(z_k'\in\{0,1\}^M,\quad{}k\in\{1,\ldots,K\}\) (1 : 연합에 있는 특징, 0 : 연합에 없는 특징)
• 각 \(z'_k\)에 대한 예측값을 얻기 전 먼저 \(z'_k\)를 원래의 feature 값으로 변환하여 모델 \(f\): \(f(h_x(z'_k))\)를 통해 예측값을 얻는다.
• Kernel SHAP로 각 \(z'_k\)에 대한 가중치를 계산한다.
• 가중 선형 모델에 적합한다.
• 선형 모델의 계수인 Shaply value를 반환한다.

동전 뒤집기를 통해 모든 값이 0과 1이 될 때까지 반복하여 무작위 연합을 만들 수 있다. 예를 들어 (1, 0, 1, 0)의 벡터는 첫 번째와 세 번째 특징의 연합이라는 것을 의미한다. K개의 표본 연합은 회귀 모형의 데이터 세트가 되고, 회귀 모형의 목표는 연합에 대한 예측입니다. (여기서 “이진수로 구성된 연합에 대해 모델이 학습되지 않았는데 어떻게 예측을 할 수 있지?”라는 생각을 할 수 있다) 특성값의 연합으로부터 유효한 데이터의 관측치를 얻기 위해서는 \(h_x:\{0,1\}^M\rightarrow\mathbb{R}^p\)일때 \(h_x(z')=z\)인 함수가 필요하다. 함수 \(h_x\)는 이진 연합에서 1을 설명하고자 하는 관측치 x의 해당 값에 매핑한다. Tabular data 경우 0을 데이터에서 샘플링 한 또 다른 관측치의 값에 매핑한다. 이는 “특성값이 없음”과 “특성값이 데이터의 랜덤한 특성값으로 대체 됨”과 동일함을 의미한다. 아래 그림이 tabular data의 경우 연합에서 특성값으로의 매핑이 어떻게 되는지 보여주는 예시이다.

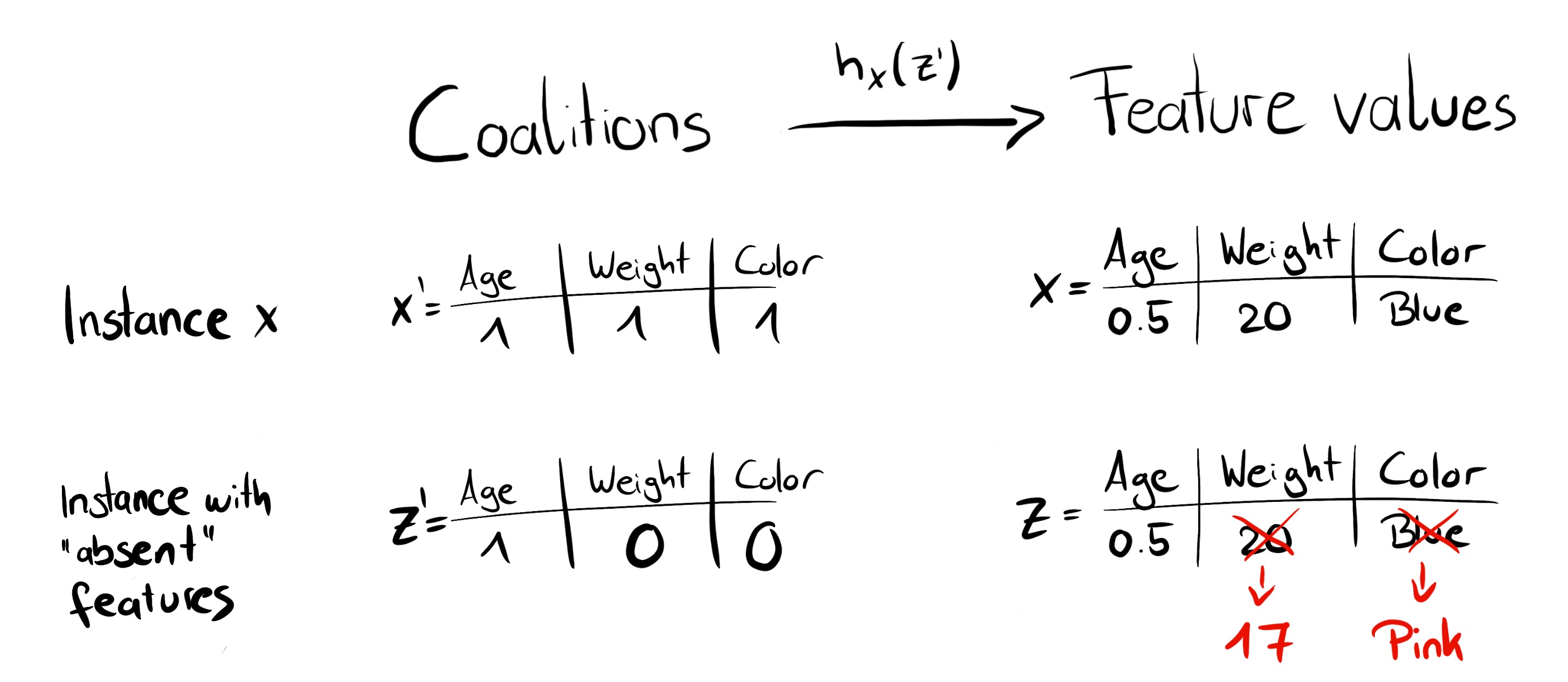
함수 h_x 는 coalition을 valid instance에 매핑한다. 특성이 있는 (1)의 경우, h_x는 x의 특성값에 매핑된다. 특성이 없는 (0)의 경우, h_x는 무작위로 샘플링된 데이터 instance의 값에 매핑된다. 

원래 수식적으로 보자면 \(h_x\)는 특성이 없는 경우 특성이 있는 경우에서 고려하여 추출한다.

\[f(h_x(z'))=E_{X_C|X_S}[f(x)|x_S]\]

여기서 \(X_C\)는 특성이 없는 집합이고\(X_S\)는 특성이 있는 집합이다. 그러나, 위에서 정의한 것처럼 tabular 데이터에서는 \(X_C\)와 \(X_S\)는 서로 독립으로 취급하여 한계 분포(marginal distribution)에 대해서 통합한다.

\[f(h_x(z'))=E_{X_C}[f(x)]\]

한계 분포에서 표본을 뽑는다는 것은 특성이 있는 것과 없는 것 사이의 의존적인 관계를 무시하는 것을 뜻한다. KernelSHAP은 즉 permutation을 기반으로 하는 해석 방법과 마찬가지로 같은 문제를 가지고 있다. 측정치는 어떤 관측치에 뜻하지 않은 큰 가중치를 부여하게 될 수도 있기 때문에 결과를 신뢰하지 못하게 될 수도 있다. 그러나 이후 언급하겠지만 의사결정 나무를 기반으로 하는 앙상블 방법에 적용되는 TreeSHAP의 경우 이러한 문제 없이 사용할 수 있다.

함수 h_x는 슈퍼 픽셀의 연합을 이미지로 매핑한다. (슈퍼 픽셀은 픽셀의 그룹을 의미한다). 특성이 있는 (1) 경우, 원본 이미지의 해당 부분을 반환한다. 특성이 없는 (0) 경우, 해당 부분을 회색으로 만든다. (주변 픽셀이나 비슷한 픽셀의 평균적인 색으로 할당하는 것은 옵션이다.)

LIME과 가장 큰 차이점은 회귀 모델에서 관측치의 가중치이다. LIME은 원래 관측치와 얼마나 가까운지에 따라 관측치에 가중치를 부여한다. 연합 벡터에 0이 많을수록 LIME의 가중치가 작아진다. SHAP은 c 연합을 Shapley value 추정에서 얻을 수 있는 가중치에 따라 샘플링된 관측치에 가중치를 부여한다. 작은 연합 (1이 적음) 및 큰 연합 (1이 많음)은 큰 가중치를 갖는다. 그 말은 다음과 같이 얘기할 수 있다. 각 관측치에 특성에 대해 고유한 영향력을 구할 수 있다면 모든 특성을 모두 파악할 수 있다. 만약 연합이 단일 특성으로 구성된 경우 예측값에 대한 단일 특성의 고유 영향력을 얻을 수 있다. 연합의 모든 구성이 하나의 특성으로 구성된 경우에 해당 특성의 총 영향력(고유 영향력에 변수 간 상호 작용 더한 값)에 대해 얻을 수 있다. 연합의 절반만 특성이 있는 경우 이러한 조합이 무수히 많을 수 있기 때문에 각각의 특성의 영향력을 조금밖에 얻을 수 없다.

정해진 규칙에 따른 가중치를 통해 Shapley value를 얻기 위해 Lundberg는 SHAP kernel을 제안했다.

\[\pi_{x}(z')=\frac{(M-1)}{\binom{M}{|z'|}|z'|(M-|z'|)}\]

여기서 M은 연합의 최대 크기이고 $$

z’

\(는 관측치\)z’$$에 존재하는 특성 수이다. Lundberg와 Lee는 kernel weight을 가진 선형 회귀 모델이 Shapley Value을 추정할 수 있다고 얘기한다.

연합 데이터로 SHAP kernel 조건과 함께 LIME을 사용할 경우 LIME은 Shapley Value도 추정할 수 있다

우리는 연합 샘플링을 조금 더 효율적으로 할 수 있다. 가장 작거나 큰 연합은 가장 큰 가중치를 얻는다. 우리는 무작위로 연합에서 샘플링하기보다 이 큰 가중치들만 가지고 샘플링 자원(budget) K를 사용하여 Shapley value를 얻을 수 있다. 1부터 M-1까지 총 2 x M 개의 연합을 만들 수 있다. 우리가 충분한 자원이 남았다면 (현재는 K-2M), 두 개부터 M-2개 등의 연합을 더 포함할 수 있다. 남은 연합의 크기로부터 우리는 재조정한 가중치를 뽑을 수 있다.

우리는 데이터와 목표값, 가중치를 가지고 아래와 같이 가중 선형 회귀 모델을 만들 수 있다.

\[g(z')=\phi_0+\sum_{j=1}^M\phi_jz_j'\]

다음으로는 손실 함수 L을 최적화하여 선형 모델 g를 훈련한다.

\[L(f,g,\pi_{x})=\sum_{z'\in{}Z}[f(h_x(z'))-g(z')]^2\pi_{x}(z')\]

여기서 z는 학습할 데이터이다. 선형 모델을 최적화하기위해 오자제곱합을 사용하는 것이 일반적이다. 모델의 추정된 계수인 \(\phi_j\)가 Shapley Value이다.

선형 회귀로 설정함으로써, 회귀에 대한 standard tools를 사용할 수 있다. 예를 들어, Sparse model에 정규화를 추가할 수 있다. 또한, 손실 함수 L에 L1 페널티를 추가하여, Sparse에 대한 설명을 할 수 있다. (그러나 계수가 여전히 유효한 Shapley value인지 확신할 수 없다.)

4. TreeSHAP

Lundberg는 decision trees, random forests and gradient boosted trees와 같은 트리 기반 기계 학습 모델을 위한 SHAP의 변형인 TreeSHAP를 제안했다². Tree SHAP은 빠르고 정확한 Shapley value를 계산하며 특성이 종속인 경우 Shapley Value를 정확하게 추정한다. 이에 비해 KernelSHAP는 계산 비용이 많이 들고 실제 Shapley value만 근사하게 추정한다.

TreeSHAP은 얼마나 빠를까? 정확한 Shapley value 계산을 하는데 모델 복잡도를 \(O(TL2^M)\)에서 \(O(TLD^2)\)로 줄일 수 있다. 여기서 T는 트리의 개수, L은 모든 트리의 최대 나뭇잎(leave) 수 그리고 D는 모든 트리의 최대 깊이(depth)이다.

TreeSHAP는 정확한 조건부 기대치( $$E_{X_S

X_C}(f(x)

x_S)\()를 추정한다. 어떻게 단일 트리, 관측치 x 및 특성 서브 셋 S로 예상되는 예측을 계산할 수 있는지에 대한 방법(intuition)을 얘기해보도록 하겠다. 모든 특성에 조건을 적용한 경우(즉, S가 모든 특성의 집합인 경우), 어떤 관측치 x가 속해있는 노드로부터의 예측은 예측값을 예상할 수 있다. 어떤 특성에 대해 조건이 없는 경우(즉, 부분 집합 S가 비어 있다면) 모든 터미널 노드의 가중 평균 예측을 사용한다. 또한 S에 모든 특성이 아닌 일부 특성이 포함된 경우, 도달할 수 없는 노드의 예측은 무시한다. '도달할 수 없음'은 노드로 연결되는 결정 경로가 \)X_S$$ 값과 일치하지 않음을 의미한다. 나머지 터미널 노드에서 노드 크기 (즉, 해당 노드의 학습 샘플 수)에 따라 가중치가 적용된 예측의 평균을 낸다. 남은 터미널 노드의 평균은 노드 당 관측치 수에 따라 가중치가 부여되며 주어진 S에 대해 예상되는 예측값이다. 문제는 특성값의 가능한 각 부분집합 S에 대해 이 절차를 모두 적용해야 한다는 것이다. 다행히 TreeSHAP은 연산시간이 지수적(exponential)으로 증가하기보다는 배수(polynomial)로 증가한다. 기본 아이디어는 가능한 모든 부분집합 S를 동시에 트리의 하위 노드로 출발하는 것이다. 이때 각 의사 결정 노드에서 부분집합 수를 기억해야 한다. 이는 상위 노드의 부분집합과 어떤 특성으로 분할하는지에 따라 달라진다.

예를 들어, 특성 x3이 있는 트리의 첫 번째 분할에서 특성 x3를 포함하는 모든 부분집합이 하나의 노드(x가 가는 노드)로 이동한다. 특성 x3를 포함하지 않은 부분집합은 가중치가 감소 된 양쪽 노드로 이동한다. 그러나 크기가 다른 부분집합의 가중치는 서로 다르기 때문에 각각의 노드에 있는 부분집합의 전체 가중치를 전부 기억하고 있어야 한다. 이런 점 때문에 계산식이 더 복잡하게 된다. 연산량은 트리가 늘어남에 따라 더 커질 수 있다.

Shapley value의 additivity 속성 덕분에 트리 앙상블의 Shapley value는 개별 트리의 Shapley value를 (가중) 평균으로 구할 수 있다.

5. Advantages

SHAP는 Shapley value를 계산하기 때문에 Shapley Value의 모든 장점이 적용된다. SHAP는 게임 이론에서 확고한 이론적 기반을 가지고 있다. 또한 예측은 특성값 사이에 고르게 분포되어 있다. 예측과 평균 예측을 비교하는 대조적인 설명을 얻을 수 있다.

SHAP은 LIME과 Shapley value를 연결한다. 따라서 두 방법을 더 잘 이해하는 데 매우 유용하다. 해석 가능한 기계학습 분야를 unify 하는 데도 도움이 된다.

SHAP은 트리 기반 모델을 빠르게 구현한다. SHAP이 인기 있는 이유는 Shapley value는 SHAP에 비해 계산속도 느리기 때문이라고 생각한다.

빠른 계산속도는 글로벌 모델 해석에 필요한 많은 Shapley value를 계산하는 것을 가능하게 한다. 글로벌 해석 방법에는 feature importance, feature dependence, interactions, clustering and summary plots가 포함된다. Shapley value는 전역 해석의 “atomic unit”이기 때문에 SHAP와 함께 전역 해석은 지역 설명과 일관되다. LIME을 지역 설명(local explanations) 및 부분 의존도 그림(partial dependence plots) 및 전역 설명(global explanations)에 대한 permutation feature importance에 사용할 경우 공통 기초가 결여된다.

6. Disadvantages

Kernel SHAP는 속도가 느리기 때문에 많은 인스턴스에 대해 Shapley value를 계산하려는 경우 사용할 수 없다. 또한 global SHAP 중 SHAP feature importance는 많은 인스턴스의 Shapley value를 계산해야 한다.

Kernel SHAP는 특성 의존성(feature dependence)을 무시한다. 대부분의 다른 순열 기반 해석 방법 또한 이 문제를 가지고 있다. 특성값을 랜덤 인스턴스의 값으로 대체하면 대개 marginal distribution에서 무작위로 표본을 추출하기가 더 쉽다. 그러나 특성이 종속인 경우(즉, 상관관계), 이는 예상하지 못한 data point에서 너무 많은 가중치를 부여하게 된다. Tree SHAP는 조건부 예측을 명시적으로 모델링하여 이 문제를 해결한다.

Shapley value의 단점은 또한 SHAP에도 적용된다. Shapley value는 잘못 해석될 수 있으며, 새로운 데이터를 계산할 때 데이터 대한 액세스가 필요하다(TreeSHAP 제외)

---